Skip to contents

Models without compartments

2024-10-18

Source: vignettes/extra/dollar-pred.Rmd
dollar-pred.Rmd

This vignette introduces a new formal code block for writing models where there are no compartments. The block is named after the analogous NONMEM block called $PRED. This functionality has always been possible with mrgsolve, but only now is there a code block dedicated to these models. Also, a relaxed set of data set constraints have been put in place when these types of models are invoked.

Example model

As a most-basic model, we look at the pred1 model in modlib()

mod <- modlib("pred1")

The model code is

$PROB
An example model expressed in closed form
$PARAM B = -1, beta0 = 100, beta1 = 0.1
$OMEGA 2 0.3
$PRED
double beta0i = beta0 + ETA(1);
double beta1i = beta1*exp(ETA(2));
capture Y = beta0i + beta1i*B;

This is a random-intercept, random slope linear model. Like other models in mrgsolve, you can write parameters ($PARAM), and random effects ($OMEGA). But the model is actually written in $PRED.

When mrgsolve finds $PRED, it will generate an error if it also finds $MAIN, $TABLE, or $ODE. However, the code that gets entered into $PRED would function exactly as if you put it in $TABLE.

In the example model, the response is a function of the parameter B, so we’ll generate an input data set with some values of B

data <- tibble(ID = 1, B = exp(rnorm(100, 0,2)))

head(data)
## # A tibble: 6 × 2
##      ID     B
##   <dbl> <dbl>
## 1     1 5.61 
## 2     1 0.749
## 3     1 0.322
## 4     1 0.150
## 5     1 2.06 
## 6     1 4.06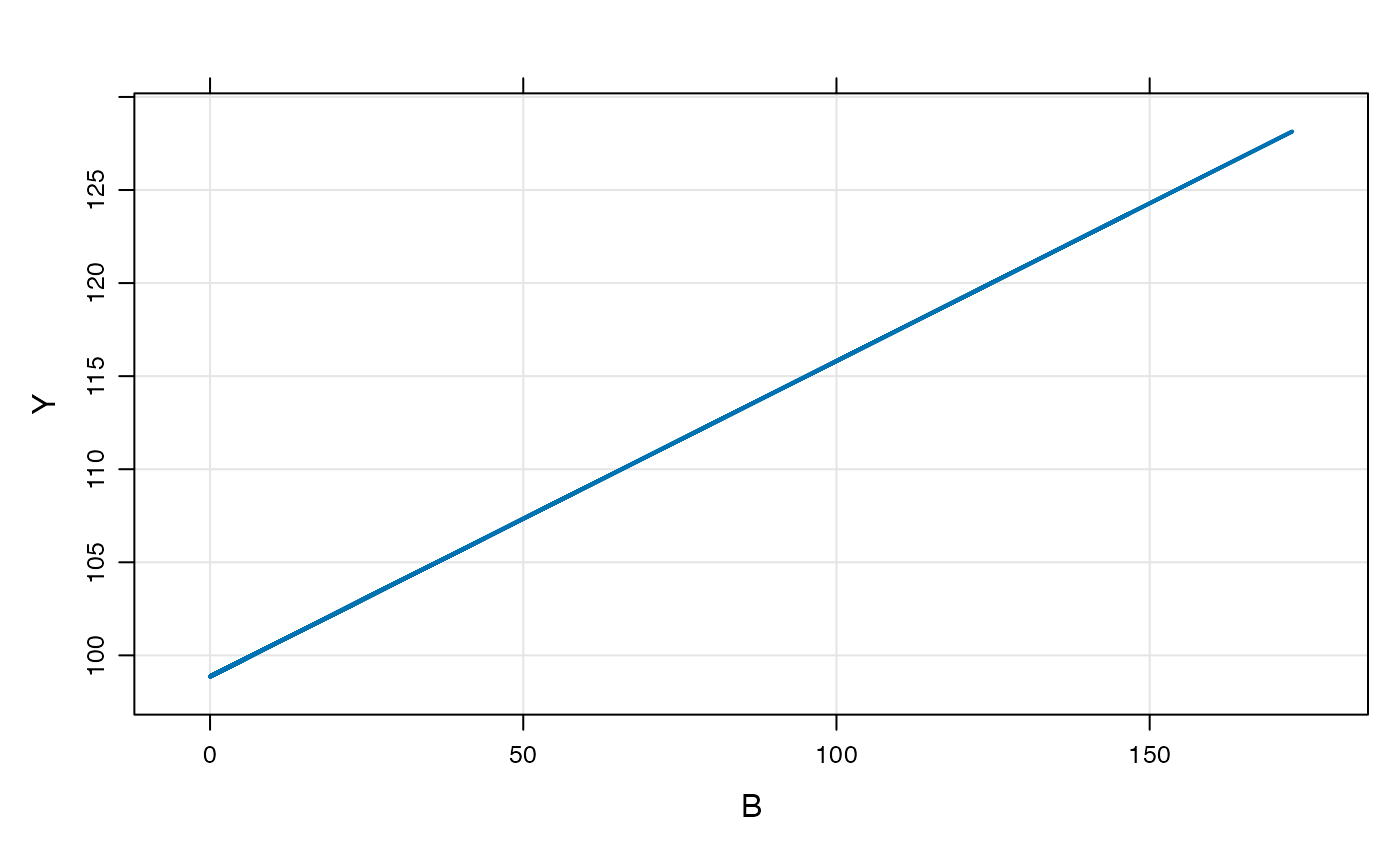
out <- mrgsim_d(mod, data, carry_out = "B")

plot(out, Y~B)

Like other models, we can simulate from a population

df <- map_df(1:30, ~ tibble(ID = .x, B = seq(0,30,1)))

head(df)
## # A tibble: 6 × 2
##      ID     B
##   <int> <dbl>
## 1     1     0
## 2     1     1
## 3     1     2
## 4     1     3
## 5     1     4
## 6     1     5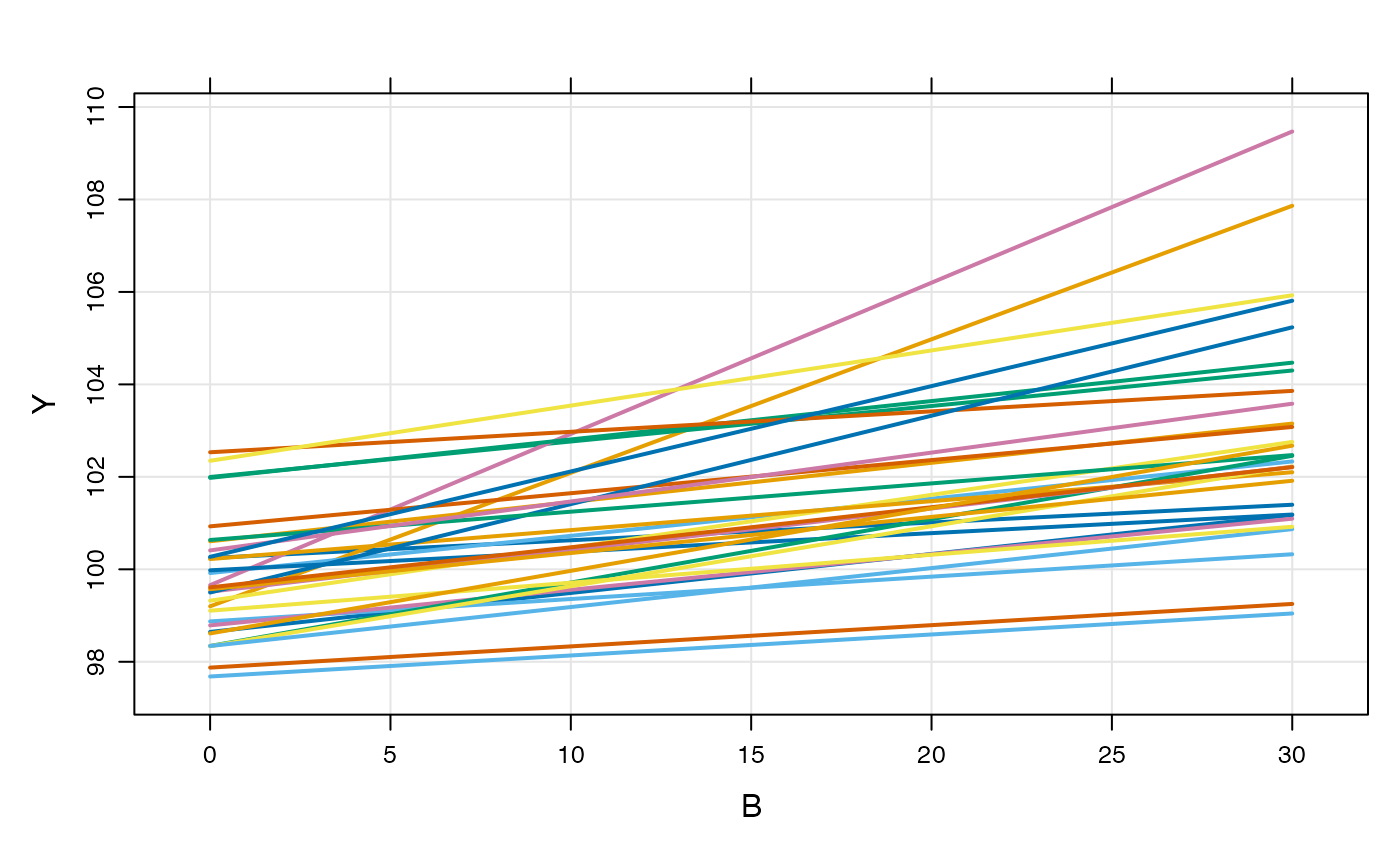
mod %>% 
  data_set(df) %>% 
  mrgsim(carry_out = "B") %>%
  plot(Y ~ B)

PK/PD Model

Here is an implementation of a PK/PD model using $PRED

In this model

  • Calculate CL as a function of WT and a random effect
  • Derive AUC from CL and DOSE
  • The response (Y) is a calculated from AUC and the Emax model parameters
code <- '
$PARAM TVCL = 1, WT = 70, AUC50 = 20, DOSE = 100, E0 = 35, EMAX = 2.4

$OMEGA 1

$SIGMA 100

$PRED
double CL = TVCL*pow(WT/70,0.75)*exp(ETA(1));
capture AUC = DOSE/CL;
capture Y = E0*(1+EMAX*AUC/(AUC50+AUC))+EPS(1);
'
mod <- mcode_cache("pkpd", code)

To simulate, look at 50 subjects at each of 5 doses

set.seed(8765)

data <- 
  expand.idata(DOSE = c(30,50,80,110,200), ID = 1:50) %>% 
  mutate(WT = exp(rnorm(n(),log(80),1)))

head(data)
##   ID DOSE        WT
## 1  1   30  39.67626
## 2  2   50  36.27156
## 3  3   80  60.14424
## 4  4  110  81.59561
## 5  5  200  22.10396
## 6  6   30 126.69565
out <- mrgsim_df(mod, data, carry_out="WT,DOSE") 

head(out)
##   ID time        WT DOSE       AUC         Y
## 1  1    0  39.67626   30 298.76467 115.82635
## 2  2    0  36.27156   50 108.78989  97.65895
## 3  3    0  60.14424   80  13.74925  52.41350
## 4  4    0  81.59561  110 186.47672 125.92038
## 5  5    0  22.10396  200 494.49076 116.76226
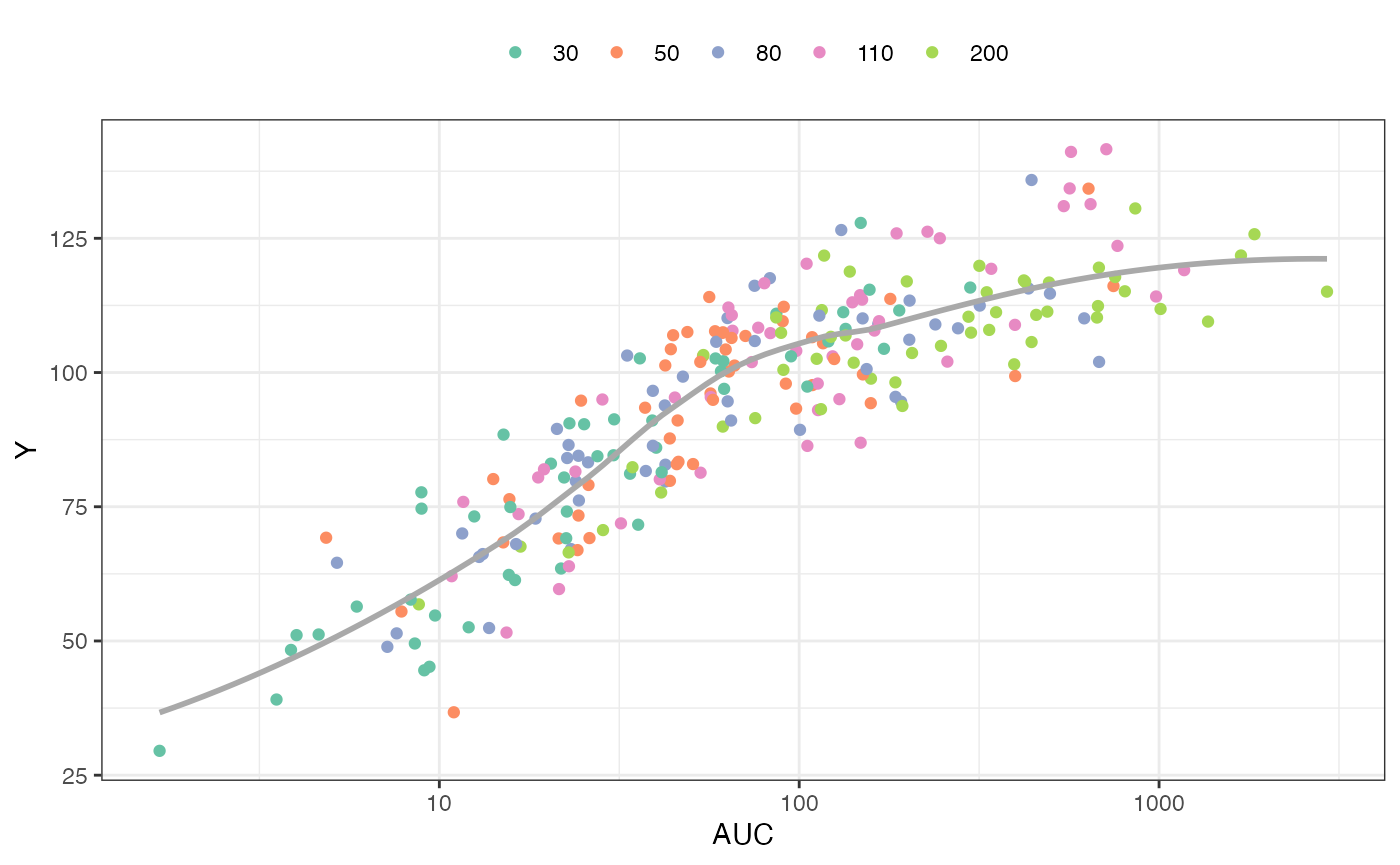
## 6  6    0 126.69565   30  22.61341  74.10551

Plot the response (Y) versus AUC, colored by dose

ggplot(out, aes(AUC, Y, col =factor(DOSE))) + 
  geom_point() + 
  scale_x_log10(breaks = 10^seq(-4, 4)) + 
  geom_smooth(aes(AUC,Y), se = FALSE, col="darkgrey") + theme_bw() + 
  scale_color_brewer(palette = "Set2", name = "") + 
  theme(legend.position = "top")