Estimate a multi-state model with mrgsolve

evtools
msm
example
draft
Author

Kyle Baron

Published

May 10, 2024

1 Introduction

This post shows how you can fit a simple multi-state model with mrgsolve. We’ll fit a model to the cav data from the msm package using both msm and mrgsolve and then compare the results.

Some references for the data and analysis include

  • Sharples, L. D., Jackson, C. H., Parameshwar, J., Wallwork, J. & Large, S. R. Diagnostic accuracy of coronary angiography and risk factors for post-heart-transplant cardiac allograft vasculopathy. Transplantation 76, 679–682 (2003). [Link]

  • Jackson, C. H. Multi-State Models for Panel Data: The msm Package for R. J. Stat. Softw. 38, 1–28 (2011). [Link]

  • Multi-state modelling in R: the msm package [Link]

This post updated July 2024 to use mrgsolve 1.5.1 which introduces a replace() function in the evt namespace (see the evtools plugin). The evt::replace() syntax is just like evt::bolus(), but we replace the the amount in the indicated compartment, rather than adding to it. This utilizes EVID = 8, a long-standing feature in mrgsolve, which can be conveniently called from within your model starting with 1.5.1.

The cav data is a “series of approximately yearly angiographic examinations of heart transplant recipients. The state at each time is a grade of cardiac allograft vasculopathy (CAV), a deterioration of the arterial walls.” (Link).

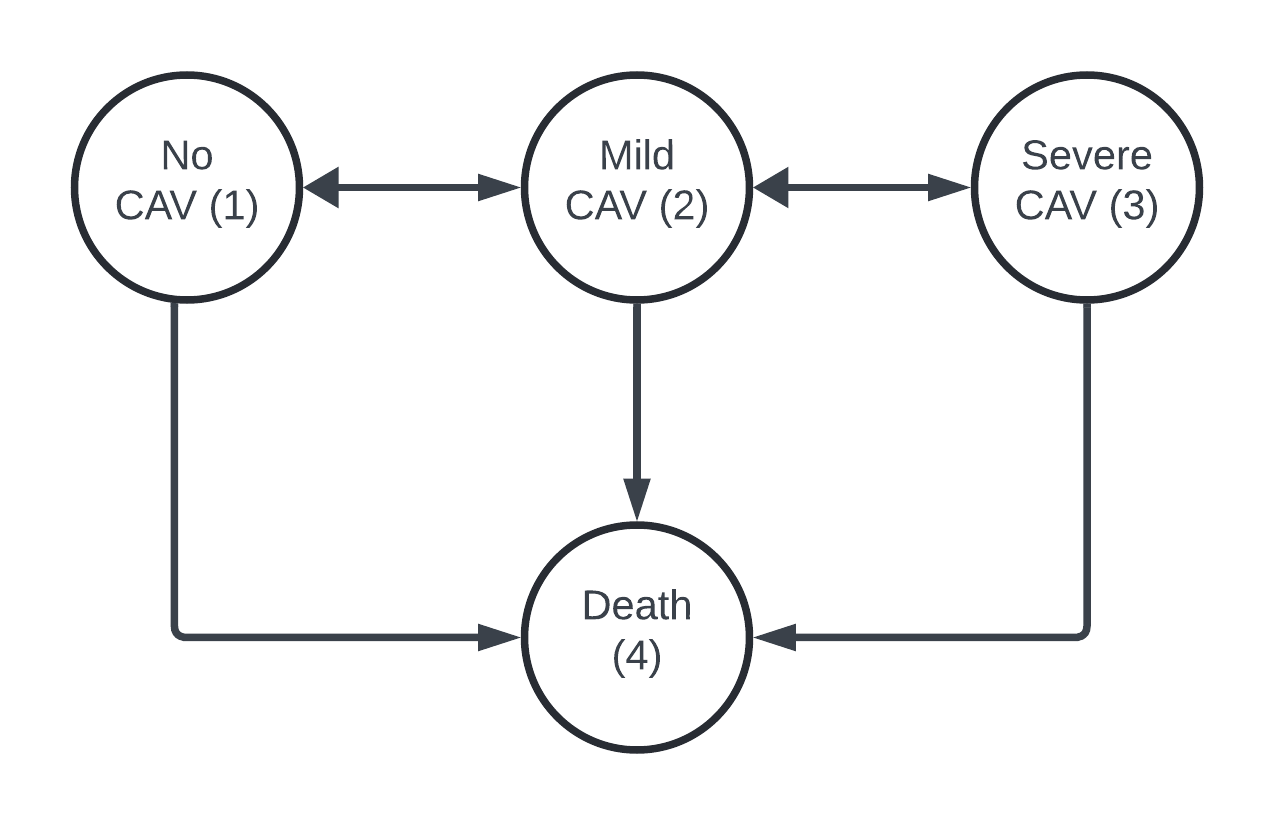
There are four states in the CAV data set

  1. No CAV
  2. Mild or moderate CAV
  3. Severe CAV
  4. Death

The data set includes 2846 observations across 622 subjects.

2 Fit the model with msm

library(msm)
library(mrgsolve)
library(dplyr)
library(minqa)
options(pillar.width = Inf)

2.1 Transition matrix

The transitions in the data set look like

statetable.msm(state, PTNUM, data=cav)
    to
from    1    2    3    4
   1 1367  204   44  148
   2   46  134   54   48
   3    4   13  107   55

We’ll follow the analysis presented by the msm package, using this transition matrix

qq <- rbind(
  c(0, 0.25, 0, 0.25), 
  c(0.166, 0, 0.166, 0.166),
  c(0, 0.25, 0, 0.25), 
  c(0, 0, 0, 0)
)
qq
      [,1] [,2]  [,3]  [,4]
[1,] 0.000 0.25 0.000 0.250
[2,] 0.166 0.00 0.166 0.166
[3,] 0.000 0.25 0.000 0.250
[4,] 0.000 0.00 0.000 0.000

This assumes that transitions between State 1 and State 3 must pass through State 2.

Transitions for CAV model. Figure adapted from https://chjackson.github.io/msm/msmcourse/theory.html and Sharples et al. 2003.

2.2 Call to fit the model

Fit the model with deathexact = 4, indicating that 4 (death) is an absorbing state whose time of entry is known exactly, but with unknown transient state just prior to entering.

cav.msm <- msm(
  state ~ years, 
  subject = PTNUM, 
  data = cav,
  qmatrix = qq, 
  deathexact = 4
)

cav.msm

Call:
msm(formula = state ~ years, subject = PTNUM, data = cav, qmatrix = qq,     deathexact = 4)

Maximum likelihood estimates

Transition intensities
                  Baseline                    
State 1 - State 1 -0.17037 (-0.19027,-0.15255)
State 1 - State 2  0.12787 ( 0.11135, 0.14684)
State 1 - State 4  0.04250 ( 0.03412, 0.05294)
State 2 - State 1  0.22512 ( 0.16755, 0.30247)
State 2 - State 2 -0.60794 (-0.70880,-0.52143)
State 2 - State 3  0.34261 ( 0.27317, 0.42970)
State 2 - State 4  0.04021 ( 0.01129, 0.14324)
State 3 - State 2  0.13062 ( 0.07952, 0.21457)
State 3 - State 3 -0.43710 (-0.55292,-0.34554)
State 3 - State 4  0.30648 ( 0.23822, 0.39429)

-2 * log-likelihood:  3968.798

The msm package provides some visualization of the result

plot(cav.msm)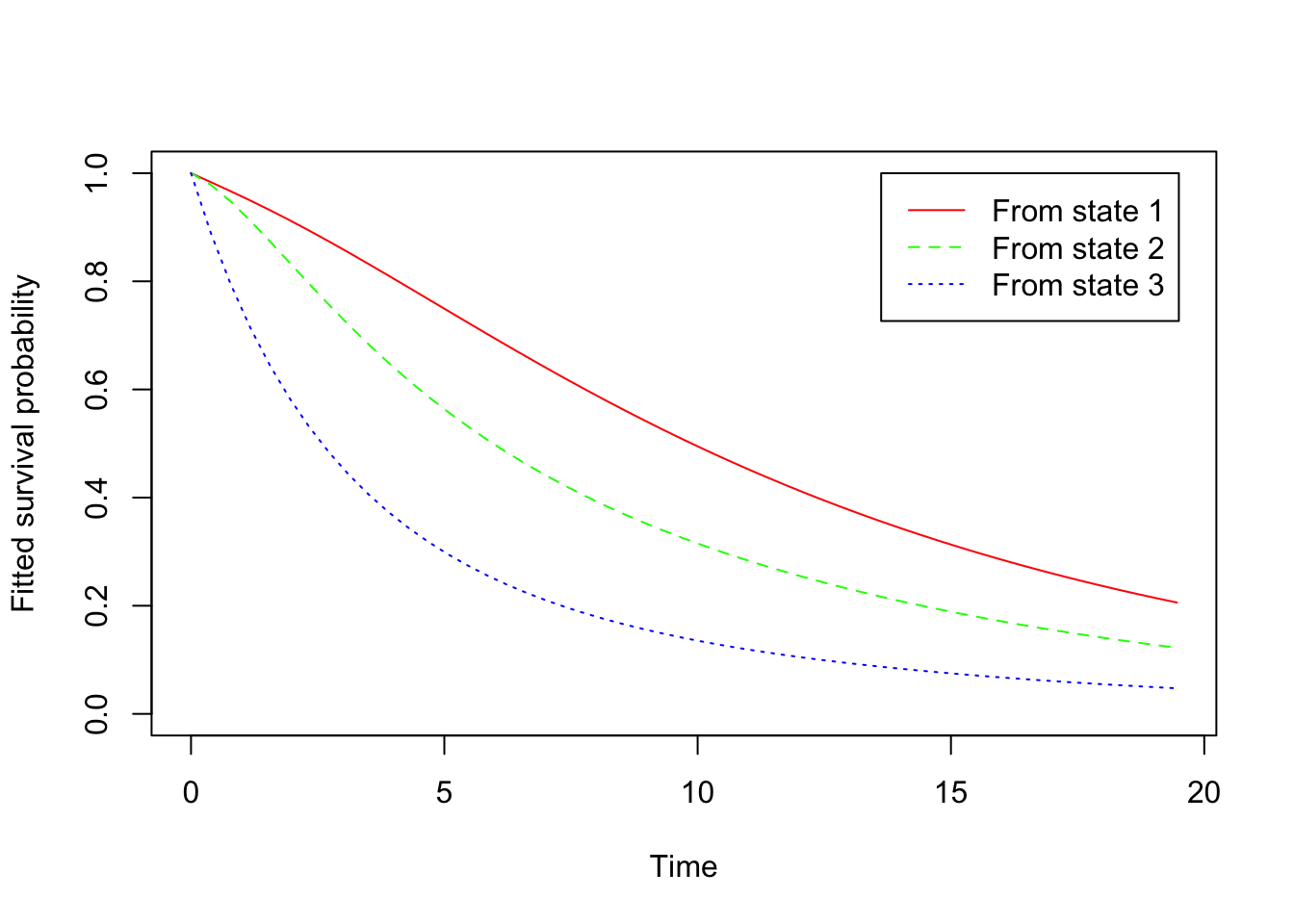

3 Now use mrgsolve

3.1 Data

Modify the data to use with mrgsolve, adding columns for ID and TIME

data <- rename(
  as_tibble(cav), 
  ID = PTNUM, 
  time = years
)

The data set is really fairly simple

head(data, n = 4)
# A tibble: 4 × 10
      ID   age  time  dage   sex pdiag cumrej state firstobs statemax
   <int> <dbl> <dbl> <int> <int> <fct>  <int> <int>    <int>    <dbl>
1 100002  52.5  0       21     0 IHD        0     1        1        1
2 100002  53.5  1.00    21     0 IHD        2     1        0        1
3 100002  54.5  2.00    21     0 IHD        2     2        0        2
4 100002  55.6  3.09    21     0 IHD        2     2        0        2
  • The state column marks the state at the examination, ranging from 1 (no CAV) to 3 (severe CAV) as well as State 4 (death).
  • Every subject starts in state 1
  • There are also some covariates that we won’t use in this example

You can also verify that there are no records in the data set to reset or dose into any compartment; we’ll handle all of that from inside the model.

3.2 Model

Set up a model with the four states

msm-cav.mod
$PLUGIN autodec evtools

$CMT @annotated
A1 : 0 : No CAV
A2 : 0 : Mild or moderate CAV
A3 : 0 : Severe CAV
A4 : 0 : Death

$PARAM @annotated
k12 : 0.1 : None to mild or moderate
k21 : 0.1 : Mild or moderate to none
k23 : 0.1 : Mild or moderate to severe
k32 : 0.1 : Severe to mild or moderate
k14 : 0.1 : None to death
k24 : 0.1 : Mild or moderate to death
k34 : 0.1 : Severe to death

$INPUT
state = 1

$PK
A1_0 = 1;

$DES
dxdt_A1 = -A1 * k12 + A2 * k21 - A1 * k14;
dxdt_A2 =  A1 * k12 - A2 * k21 - A2 * k23 + A3 * k32 - A2 * k24;
dxdt_A3 =  A2 * k23 - A3 * k32 - A3 * k34;
dxdt_A4 =  A1 * k14 + A2 * k24 + A3 * k34;

$ERROR
if(EVID != 0) return;

if(state==1) Y = A1;
if(state==2) Y = A2;
if(state==3) Y = A3;
if(state==4) Y = A1 * k14 + A2 * k24 + A3 * k34;

for(int st = 1; st <= 4; ++st) {
  evt::replace(self, 0, st);
}
evt::bolus(self, 1, state);

$CAPTURE Y

The key to this model is the evt::replace() function, which will reset all compartments to 0 when there is an examination and then initialize the appropriate compartment with a 1 based on the value of state in the data set. We do this with a simple for loop in C++. The replace() functionality is available in the evtools plugin starting with mrgsolve 1.5.1. More on evtools in the mrgsolve user guide.

3.3 Call to fit the model

Load the model and set up for estimation

mod <- mread("msm-cav.mod")

The initial estimates will be whatever we wrote into the model file

theta <- as.numeric(param(mod))
theta <- theta[grep("^k", names(theta))]
tnames <- names(theta)

This function takes in a set of parameters and returns the -2 log-likelihood returned from the model.

ofv <- function(p, data) {
  p <- lapply(p, exp)
  names(p) <- tnames
  mod <- param(mod, p)
  out <- mrgsim_q(mod, data)
  -2*sum(log(out$Y))
}

Use minqa::newuoa() to fit the model

fit <- newuoa(
  par = log(theta), 
  fn = ofv, 
  data = data, 
  control = list(iprint = 1)
)
start par. =  -2.302585 -2.302585 -2.302585 -2.302585 -2.302585 -2.302585 -2.302585 fn =  4208.405 
At return
eval: 247 fn:      3968.7979 par: -2.05671 -1.49120 -1.07120 -2.03544 -3.15859 -3.21225 -1.18267

This takes 4 to 4.5 seconds on my MacBook M1 Pro.

4 Compare msm and mrgsolve results

The final objective function values for the msm and mrgsolve fits are similar

fit$fval
[1] 3968.79787942
cav.msm$minus2loglik
[1] 3968.79789305

Compare estimated transition intensities (there might be a naming issue on the cav.msm estimates, but I think the values match up).

est <- exp(fit$par)

names(est) <- tnames

est %>% sort()
       k24        k14        k12        k32        k21        k34        k23 
0.04026573 0.04248539 0.12787425 0.13062362 0.22510161 0.30645974 0.34259570 
exp(cav.msm$estimates) %>% sort()
     qbase      qbase      qbase      qbase      qbase      qbase      qbase 
0.04021023 0.04250042 0.12787033 0.13062235 0.22511913 0.30647512 0.34261129