Update: Validate translation from NONMEM

With mrgsolve version 1.0.8, there is a more complete way to validate your model against a completed NONMEM estimation run.

validation
Author

Kyle Baron

Published

March 6, 2023

1 Introduction

I wrote a post in May 2022 about using NONMEM-generated PRED from a completed estimation run to validate the coding of the equivalent model in mrgsolve. This post will show you how to do a similar validation, but this time using IPRED to validate the translation.

To help with the big picture, the steps are

  1. Read in the model estimation data set
  2. Read in NONMEM $TABLE outputs which include IPRED and all the model ETA values
  3. Join the table outputs to the model estimation data set
  4. Simulate from the candidate mrgsolve model, using the etasrc = "data.all" argument to mrgsim(), new in version 1.0.8
  5. Compare NONMEM-generated IPRED against mrgsolve-generated IPRED

I’ll detail these steps in the following sections or you can jump to the complete workflow in Section 7.

You can get more information on how this all works in the mrgsim() help topic

?mrgsim

with mrgsolve 1.0.8 installed or check here.

2 Setup

library(mrgsolve)
library(readr)
library(dplyr)
library(here)
library(glue)

3 Leveraging outputs from NONMEM for validation

3.1 Population-level predictions

The basic idea from the previous post was to use PRED which is generated by NONMEM for output in your $TABLE files.

tab1 <- read_table("model/pk/106/106.tab", skip = 1)

head(tab1)
# A tibble: 6 × 8
    NUM IPRED    NPDE   CWRES    DV  PRED    RES    WRES
  <dbl> <dbl>   <dbl>   <dbl> <dbl> <dbl>  <dbl>   <dbl>
1     1   0    0       0        0     0    0      0     
2     2  68.5 -0.633  -0.512   61.0  60.6  0.422 -0.533 
3     3  90.8  0.403   0.126   91.0  78.5 12.4    0.142 
4     4  97.3  1.68    1.44   122.   83.0 39.2    1.63  
5     5  96.7  1.71    1.69   126.   82.2 43.9    1.91  
6     6  88.7 -0.0334 -0.0527  84.7  75.5  9.20  -0.0941

This comes automatically when you create $TABLE outputs unless you suppress it with the NOAPPEND option.

PRED is the population-predicted value or the prediction with all ETA (\(\eta\)) and EPS (\(\epsilon\)) set to 0. When we validate a model based on PRED, we can verify several different aspects of the model, including handling of the data set (e.g. observations and dosing interventions), the covariate model, and the coding of the differential equations to name a few. What this approach doesn’t check is the placement of the \(\eta\)s in the model.

3.2 Individual-level predictions

Notice we also have IPRED, or the individual-predicted value, in the $TABLE output shown above. I put IPRED into the output and it’s a common practice to do this.

106.ctl
$ERROR
IPRED = A(2)/V2

$TABLE IPRED FILE = 106.tab

The IPRED is a model prediction like PRED, but it includes the individual \(\eta\) generated by NONMEM. Note that these \(\eta\) are not random draws from \(\Omega\); but rather they are post-hoc \(\eta\) values for specific individuals, conditional on each individual’s data in the problem. If we can validate against IPRED rather than PRED, we can check all aspects of the data and model that we were checking with PRED, but also check the \(\eta\) placements as well, including any transformations of \(\eta\).

To get \(\eta\) into the output, I wrote

106.ctl
$TABLE ETAS(1:LAST) FILE = 106par.tab

This will give outputs ETA1, ETA2, ETA3 etc. In this example, I put these in a separate $TABLE file, but you don’t have to do this.

tab2 <- read_table("model/pk/106/106par.tab", skip = 1)

head(tab2)
# A tibble: 6 × 9
    NUM    CL    V2     Q    V3    KA   ETA1   ETA2   ETA3
  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>  <dbl>  <dbl>  <dbl>
1     1  2.62  39.8  3.02  53.0  1.39 -0.113 -0.198 -0.144
2     2  2.62  39.8  3.02  53.0  1.39 -0.113 -0.198 -0.144
3     3  2.62  39.8  3.02  53.0  1.39 -0.113 -0.198 -0.144
4     4  2.62  39.8  3.02  53.0  1.39 -0.113 -0.198 -0.144
5     5  2.62  39.8  3.02  53.0  1.39 -0.113 -0.198 -0.144
6     6  2.62  39.8  3.02  53.0  1.39 -0.113 -0.198 -0.144

I have both tab1 and tab2 data frames keyed by a NUM column that numbers the rows of the output; this makes it easy to generate a single data frame which includes all outputs

tab <- left_join(tab1, tab2, by = "NUM")

head(tab)
# A tibble: 6 × 16
    NUM IPRED    NPDE   CWRES    DV  PRED    RES    WRES    CL    V2     Q    V3
  <dbl> <dbl>   <dbl>   <dbl> <dbl> <dbl>  <dbl>   <dbl> <dbl> <dbl> <dbl> <dbl>
1     1   0    0       0        0     0    0      0       2.62  39.8  3.02  53.0
2     2  68.5 -0.633  -0.512   61.0  60.6  0.422 -0.533   2.62  39.8  3.02  53.0
3     3  90.8  0.403   0.126   91.0  78.5 12.4    0.142   2.62  39.8  3.02  53.0
4     4  97.3  1.68    1.44   122.   83.0 39.2    1.63    2.62  39.8  3.02  53.0
5     5  96.7  1.71    1.69   126.   82.2 43.9    1.91    2.62  39.8  3.02  53.0
6     6  88.7 -0.0334 -0.0527  84.7  75.5  9.20  -0.0941  2.62  39.8  3.02  53.0
     KA   ETA1   ETA2   ETA3
  <dbl>  <dbl>  <dbl>  <dbl>
1  1.39 -0.113 -0.198 -0.144
2  1.39 -0.113 -0.198 -0.144
3  1.39 -0.113 -0.198 -0.144
4  1.39 -0.113 -0.198 -0.144
5  1.39 -0.113 -0.198 -0.144
6  1.39 -0.113 -0.198 -0.144

4 Join NONMEM outputs with the model estimation data

Now, we’ll read in the model estimation data set and join on the $TABLE outputs, again by the NUM column

nmdata <- read_csv("data/derived/analysis3.csv", na = '.')

data <- left_join(tab, nmdata, by = "NUM")

Note that we’ve put tab on the left to ensure that we only include records that were not IGNOREd by NONMEM.

This data object includes the following:

  1. The model estimation data, including dosing records, observation records and covariates
  2. All of the post-hoc \(\eta\) values
  3. The individual predicted model outputs (IPRED)
head(data)
# A tibble: 6 × 49
    NUM IPRED    NPDE   CWRES  DV.x  PRED    RES    WRES    CL    V2     Q    V3
  <dbl> <dbl>   <dbl>   <dbl> <dbl> <dbl>  <dbl>   <dbl> <dbl> <dbl> <dbl> <dbl>
1     1   0    0       0        0     0    0      0       2.62  39.8  3.02  53.0
2     2  68.5 -0.633  -0.512   61.0  60.6  0.422 -0.533   2.62  39.8  3.02  53.0
3     3  90.8  0.403   0.126   91.0  78.5 12.4    0.142   2.62  39.8  3.02  53.0
4     4  97.3  1.68    1.44   122.   83.0 39.2    1.63    2.62  39.8  3.02  53.0
5     5  96.7  1.71    1.69   126.   82.2 43.9    1.91    2.62  39.8  3.02  53.0
6     6  88.7 -0.0334 -0.0527  84.7  75.5  9.20  -0.0941  2.62  39.8  3.02  53.0
     KA   ETA1   ETA2   ETA3 C        ID  TIME   SEQ   CMT  EVID   AMT  DV.y
  <dbl>  <dbl>  <dbl>  <dbl> <lgl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1  1.39 -0.113 -0.198 -0.144 NA        1  0        0     1     1     5   0  
2  1.39 -0.113 -0.198 -0.144 NA        1  0.61     1     2     0    NA  61.0
3  1.39 -0.113 -0.198 -0.144 NA        1  1.15     1     2     0    NA  91.0
4  1.39 -0.113 -0.198 -0.144 NA        1  1.73     1     2     0    NA 122. 
5  1.39 -0.113 -0.198 -0.144 NA        1  2.15     1     2     0    NA 126. 
6  1.39 -0.113 -0.198 -0.144 NA        1  3.19     1     2     0    NA  84.7
    AGE    WT    HT  EGFR   ALB   BMI   SEX   AAG   SCR   AST   ALT    CP  TAFD
  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1  28.0  55.2  160.  114.   4.4  21.7     1  106.  1.14  11.9  12.7     0  0   
2  28.0  55.2  160.  114.   4.4  21.7     1  106.  1.14  11.9  12.7     0  0.61
3  28.0  55.2  160.  114.   4.4  21.7     1  106.  1.14  11.9  12.7     0  1.15
4  28.0  55.2  160.  114.   4.4  21.7     1  106.  1.14  11.9  12.7     0  1.73
5  28.0  55.2  160.  114.   4.4  21.7     1  106.  1.14  11.9  12.7     0  2.15
6  28.0  55.2  160.  114.   4.4  21.7     1  106.  1.14  11.9  12.7     0  3.19
    TAD  LDOS   MDV   BLQ PHASE STUDYN  DOSE  SUBJ USUBJID          STUDY       
  <dbl> <dbl> <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl> <chr>            <chr>       
1  0        5     1     0     1      1     5     1 101-DEMO-0010001 101-DEMO-001
2  0.61     5     0     0     1      1     5     1 101-DEMO-0010001 101-DEMO-001
3  1.15     5     0     0     1      1     5     1 101-DEMO-0010001 101-DEMO-001
4  1.73     5     0     0     1      1     5     1 101-DEMO-0010001 101-DEMO-001
5  2.15     5     0     0     1      1     5     1 101-DEMO-0010001 101-DEMO-001
6  3.19     5     0     0     1      1     5     1 101-DEMO-0010001 101-DEMO-001
  ACTARM    RF   
  <chr>     <chr>
1 DEMO 5 mg norm 
2 DEMO 5 mg norm 
3 DEMO 5 mg norm 
4 DEMO 5 mg norm 
5 DEMO 5 mg norm 
6 DEMO 5 mg norm

5 Simulate with etasrc = "data.all"

Now we want to use mrgsolve to simulate its version of IPRED and we’ll compare that result to the NONMEM-generated IPRED as our validation of the mrgsolve setup.

mod <- mread_cache("106.txt", project = here("model/pk"))
106.txt
[ prob ]
106-104 + COV-effects(CRCL, AGE) on CL

[ pkmodel ] cmt = "GUT,CENT,PERIPH", depot = TRUE

[ param ]
WT   = 70
EGFR = 90
ALB  = 4.5
AGE  = 35

[ nmxml ]
path = "106/106.xml"
root = "cppfile"

[ main ]
double V2WT   = log(WT/70.0);
double CLWT   = log(WT/70.0)*0.75;
double CLEGFR = log(EGFR/90.0)*THETA6;
double CLAGE  = log(AGE/35.0)*THETA7;
double V3WT   = log(WT/70.0);
double QWT    = log(WT/70.0)*0.75;
double CLALB  = log(ALB/4.5)*THETA8;

double KA  = exp(THETA1+ETA(1));
double V2  = exp(THETA2+V2WT+ETA(2));
double CL  = exp(THETA3+CLWT+CLEGFR+CLAGE+CLALB+ETA(3));
double V3  = exp(THETA4+V3WT);
double Q   = exp(THETA5+QWT);

double S2 = V2/1000.0; //; dose in mcg, conc in mcg/mL

[ table ]
capture IPRED = CENT/S2;
capture Y = IPRED * (1+EPS(1));

This model is already capturing IPRED

outvars(mod)
$cmt
[1] "GUT"    "CENT"   "PERIPH"

$capture
[1] "IPRED" "Y"

We will do this with the etasrc argument to mrgsim() which is new with version 1.0.8. etasrc lets you instruct mrgsolve to look at the data set for columns named ETA1, ETA2, etc and use those values for \(\eta\) rather than generating new, random \(\eta\) from \(\Omega\).

The simulation looks like this

out <- mrgsim(
  mod, 
  data      = data, 
  etasrc    = "data.all", 
  obsonly   = TRUE, 
  Req       = "MRG = IPRED", 
  carry_out = "NM = IPRED, PRED"
)

In the above mrgsim() call, we use Req to request the IPRED output from the mrgsolve model and we use the carry_out argument to copy the IPRED value from the input data set, the NONMEM-generated value. I’ve also asked for PRED to get copied into the output so we can compare.

head(out)
  ID TIME     NM   PRED      MRG
1  1 0.61 68.532 60.583 68.53195
2  1 1.15 90.812 78.548 90.81228
3  1 1.73 97.276 83.040 97.27646
4  1 2.15 96.738 82.222 96.73794
5  1 3.19 88.706 75.487 88.70573
6  1 4.21 78.916 67.797 78.91573

Now we have IPRED generated by mrgsolve (MRG) and by NONMEM (NM).

6 Check the result

You can check the result graphically

library(ggplot2)
pick <- filter(out, ID <= 9)
p <- ggplot(data = pick) + 
  geom_point(aes(TIME, MRG)) + 
  geom_line(aes(TIME, NM), color = "blue3") +
  ylab("IPRED") + facet_wrap(~ID, scales = "free_y") + 
  ggtitle("Points: mrgsolve, Lines: NONMEM") + theme_bw()

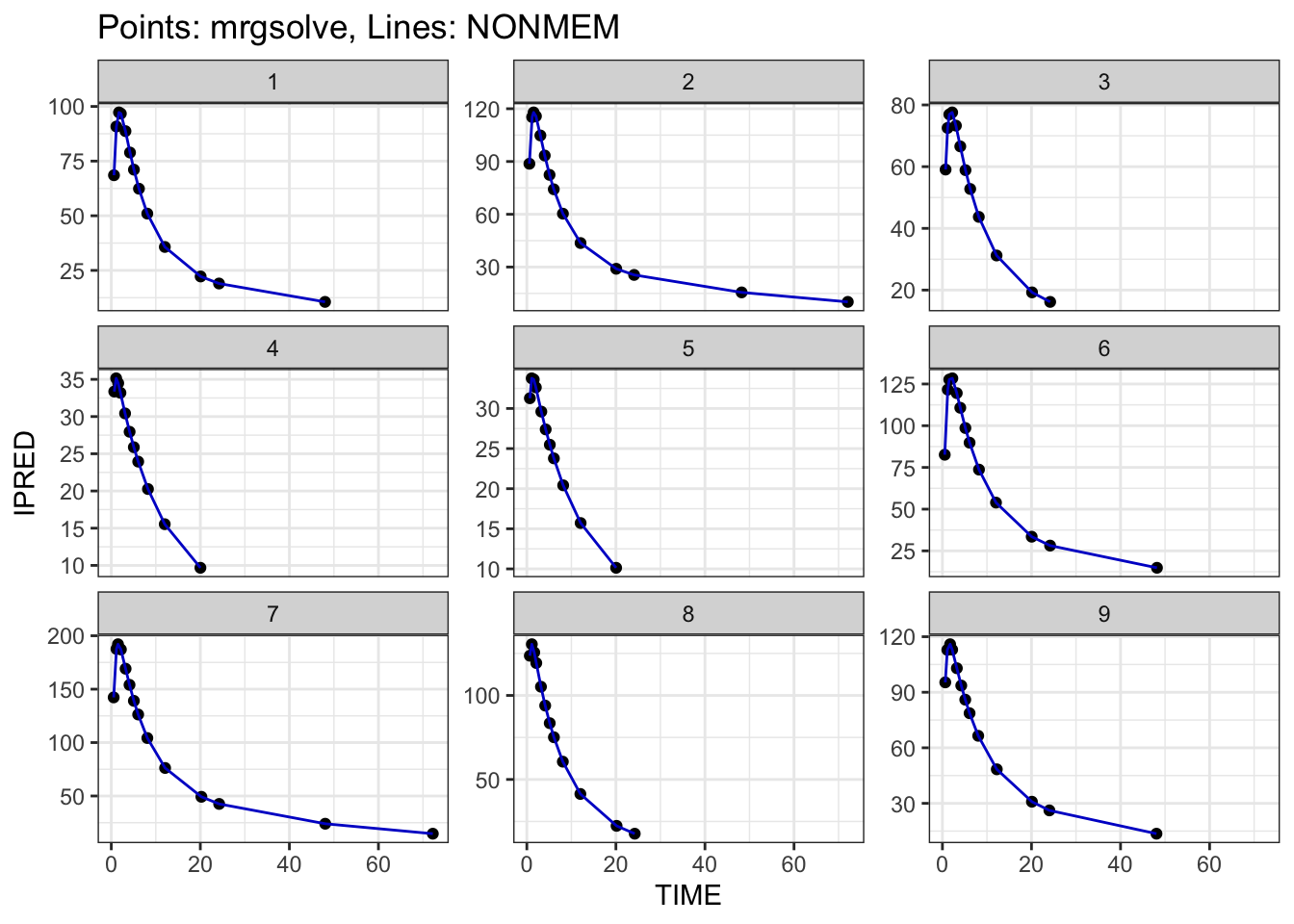
plot(out$MRG, out$NM)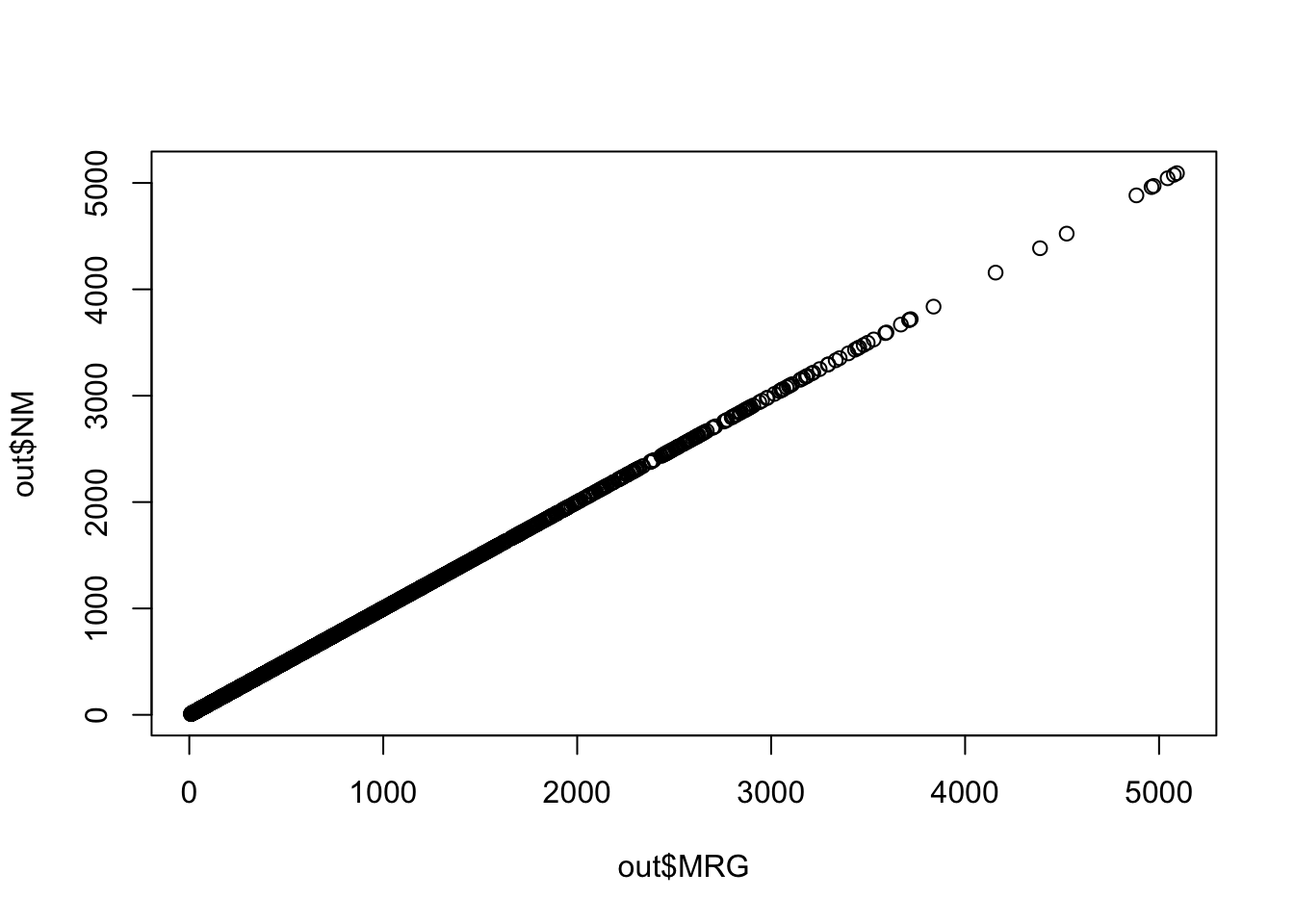

Or by some summary of the discrepancy

summary(out$MRG - out$NM)
      Min.    1st Qu.     Median       Mean    3rd Qu.       Max. 
-6.018e-02 -2.568e-03 -1.118e-05 -2.444e-05  2.710e-03  5.683e-02 
summary(100*(out$MRG - out$NM)/out$NM)
      Min.    1st Qu.     Median       Mean    3rd Qu.       Max. 
-5.731e-03 -6.735e-04 -5.256e-06  8.200e-07  7.114e-04  4.720e-03

7 Complete workflow

Here’s the complete workflow. For projects, I put this into a standalone script called validate.R and just use it to check my simulation models as model development is going on.

validate.R
run <- 106

# Read the analysis data set
nmdata <- read_csv("data/derived/analysis3.csv", na = '.')

# Read NM table outputs
tab1 <- read_table(glue("model/pk/{run}/{run}.tab"), skip = 1)
tab2 <- read_table(glue("model/pk/{run}/{run}par.tab"), skip = 1)
tab <- left_join(tab1, tab2, by = "NUM")

# Join
data <- left_join(tab, nmdata, by = "NUM")

# The mrgsolve simulation model
mod <- mread_cache(glue("{run}.txt"), project = here("model/pk"))

# Simulate
out <- mrgsim(
  mod, 
  data      = data, 
  etasrc    = "data.all", 
  obsonly   = TRUE, 
  Req       = "MRG = IPRED", 
  carry_out = "NM = IPRED"
)

# Compare
summary(out$MRG - out$NM)
      Min.    1st Qu.     Median       Mean    3rd Qu.       Max. 
-6.018e-02 -2.568e-03 -1.118e-05 -2.444e-05  2.710e-03  5.683e-02