1 About
2 One compartment model, keep it simple for now
3 First, simulate some data
4 Create input for optimization
5 Optimize
- 5.1 What is this function doing?
- 5.2 Initial estimate
6 Look at the result

library(ggplot2)
library(mrgsolve)
library(minqa)
library(dplyr)
library(magrittr)
options(mrgsolve.soloc="build")

1 About

This tutorial illustrates how to do MAP Bayes estimation with mrgsolve.
The setup was adapted from an existing project, where only a single individual was considered. With some additional R coding, it could be expanded to consider multiple individuals in a single run.

This document shows how to simulate some data and then re-estimate the MAP Bayes estimates. For clarity, just the optimization piece has been included in a separate doc map_bayes_example.html.

2 One compartment model, keep it simple for now

The model specification code below is for a one-compartment model, where mrgsolve will calculate the amount in CENT from closed-form equations
For now, $OMEGA and $SIGMA are filled with zeros; we’ll update it later
The control stream is set up so that we can either simulate the etas or pass them in. ETA(1) and ETA(2) are the etas that mrgsolve will draw from $OMEGA. ETA1 and ETA2 are fixed and known at the time of time of the simulation. The optimizer will search for values of ETA1 and ETA2 that optimize the objective function. Note that ETA1 and ETA2 must be in the parameter list for this to work
We do a trick where CL=TVCL*exp(ETA1+ETA(1)); The assumption is that either ETA1 (simulating) is zero or ETA(1) is zero (estimating)
We table out ETA(1) and ETA(2) so we can know the true (simulated) values (but not both zero and not both non-zero)
DV is output as a function of EPS(1); this will be zero until we add in values for $SIGMA. But when we’re estimating, we need to make sure that EPS(1) is zero; the prediction shouldn’t have any randomness in it (just the individual prediction based on known etas)

code <- '
$SET request=""

$PARAM TVCL=1.5, TVVC=23.4, ETA1=0, ETA2=0

$CMT CENT

$PKMODEL ncmt=1

$OMEGA 0 0
$SIGMA 0

$MAIN
double CL = TVCL*exp(ETA1 + ETA(1));
double V =  TVVC*exp(ETA2 + ETA(2));

$TABLE 
capture DV = (CENT/V)*(1+EPS(1));
capture ET1 = ETA(1);
capture ET2 = ETA(2);

'

mod <- mcode_cache("map", code)

3 First, simulate some data

$OMEGA and $SIGMA;

The result may look better or worse depending on what we choose here
These will be used to both simulate and fit the data
The cmat call makes a 2x2 matrix where the off-diagonal is a correlation (?cmat).

omega <- cmat(0.23,-0.78, 0.62)
omega.inv <- solve(omega)
sigma <- matrix(0.0032)

Just a single dose to CENT with an events object

dose <- ev(amt=750,cmt=1)

Take these times for concentration observations

sampl <- c(0.5,12,24)

Simulate

Here, we’re populating $OMEGA and $SIGMA so that the simulated data will be random
It is important to carry.out all of the items that we will need in the estimation data set (doses, evid, etc)
Using end=-1 with add=sampl makes sure that we only get observation records at the times listed in sampl

set.seed(1012) 
sim <- 
  mod %>%
  ev(dose) %>%
  omat(omega) %>%
  smat(sigma) %>%
  carry_out(amt,evid,cmt) %>%
  mrgsim(end=-1, add=sampl)

sim

. Model:  map 
. Dim:    4 x 8 
. Time:   0 to 24 
. ID:     1 
.     ID time evid amt cmt     DV    ET1     ET2
. 1:   1  0.0    1 750   1 41.067 0.5196 -0.2728
. 2:   1  0.5    0   0   0 42.749 0.5196 -0.2728
. 3:   1 12.0    0   0   0  6.932 0.5196 -0.2728
. 4:   1 24.0    0   0   0  1.375 0.5196 -0.2728

4 Create input for optimization

Using the simulated data as the starting point here
Set DV to NA for the dosing record

sim <- mutate(sim, DV = ifelse(evid==1, NA_real_, DV))

Create a data set to use in the optimization

We need to drop ET1 and ET2 since they are in the parameter list

data <- sim %>% select(-ET1, -ET2)

data

. # A tibble: 4 × 6
.      ID  time  evid   amt   cmt    DV
.   <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
. 1     1   0       1   750     1 NA   
. 2     1   0.5     0     0     0 42.7 
. 3     1  12       0     0     0  6.93
. 4     1  24       0     0     0  1.37

5 Optimize

This function takes in a set of proposed $\eta$s along with the observed data vector, the data set and a model object and returns the value of the EBE objective function

When we do the estimation, the fixed effects and random effect variances are fixed.
The estimates are the $\eta$ for clearance and volume

Arguments:

eta the current values from the optimizer
ycol the observed data column name
d the data set
m the model object
dvcol the predicted data column name
pred if TRUE, just return predicted values

5.1 What is this function doing?

get the matrix for residual error
Make sure eta is a list
Make sure eta is properly named (i.e. ETA1 and ETA2)
Copy eta into a matrix that is one row
Update the model object (m) with the current values of ETA1 and ETA2
Simulate from data set d and save output to out object
If we are just requesting predictions (if(pred)) return the simulated data
The final lines calculate the EBE objective function; see this paper for reference
Notice that the function returns a single value (a number); the optimizer will minimize this value

mapbayes <- function(eta,d,ycol,m,dvcol,pred=FALSE) {
    
  sig2 <- as.numeric(sigma)
  eta <- as.list(eta)
  names(eta) <- names(init)
  eta_m <- eta %>% unlist %>% matrix(nrow=1)
  m <-  param(m,eta)
  out <- m %>% zero_re() %>% mrgsim(data=d,output="df")
  if(pred) return(out)
  # http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3339294/
  sig2j <- out[[dvcol]]^2*sig2
  sqwres <- log(sig2j) + (1/sig2j)*(d[[ycol]] - out[[dvcol]])^2
  nOn <- diag(eta_m %*% omega.inv %*% t(eta_m))
  return(sum(sqwres,na.rm=TRUE) + nOn)
}

5.2 Initial estimate

Note again that we are optimizing the etas here

init <- c(ETA1=-0.3, ETA2=0.2)

Fit the data

newuoa is from the minqa package
Other optimizers (via optim) could probably also be used

Arguments to newuoa

First: the initial estimates
Second: the function to optimize
The other argument are passed to mapbayes

fit <- nloptr::newuoa(init,mapbayes,ycol="DV",m=mod,d=data,dvcol="DV")

Here are the final estimates

fit$par

. [1]  0.4995400 -0.3274858

Here are the simulated values

slice(sim,1) %>% select(ET1, ET2)

. # A tibble: 1 × 2
.     ET1    ET2
.   <dbl>  <dbl>
. 1 0.520 -0.273

6 Look at the result

A data set and model to get predictions; this will give us a smooth prediction line

pdata <- data %>% filter(evid==1)
pmod <- mod %>% update(end=24, delta=0.1)

Predicted line based on final estimates

pred <- mapbayes(fit$par,ycol="DV",pdata,pmod,dvcol="DV",pred=TRUE) %>% filter(time > 0)
head(pred)

.   ID time       DV ET1 ET2
. 1  1  0.1 43.82331   0   0
. 2  1  0.2 43.18567   0   0
. 3  1  0.3 42.55731   0   0
. 4  1  0.4 41.93809   0   0
. 5  1  0.5 41.32789   0   0
. 6  1  0.6 40.72656   0   0

Predicted line based on initial estimates

initial <- mapbayes(init,ycol="DV",pdata,pmod,dvcol="DV",pred=TRUE) %>% filter(time > 0)
head(initial)

.   ID time       DV ET1 ET2
. 1  1  0.1 26.13954   0   0
. 2  1  0.2 26.03811   0   0
. 3  1  0.3 25.93707   0   0
. 4  1  0.4 25.83642   0   0
. 5  1  0.5 25.73616   0   0
. 6  1  0.6 25.63629   0   0

Plot

ggplot() + 
  geom_line(data=pred, aes(time,DV),col="firebrick", lwd=1) + 
  geom_line(data=initial,aes(time,DV), lty=2, col="darkgreen", lwd=1) + 
  geom_point(data=data %>% filter(evid==0), aes(time,DV), col="darkslateblue",size=3) + 
  theme_bw()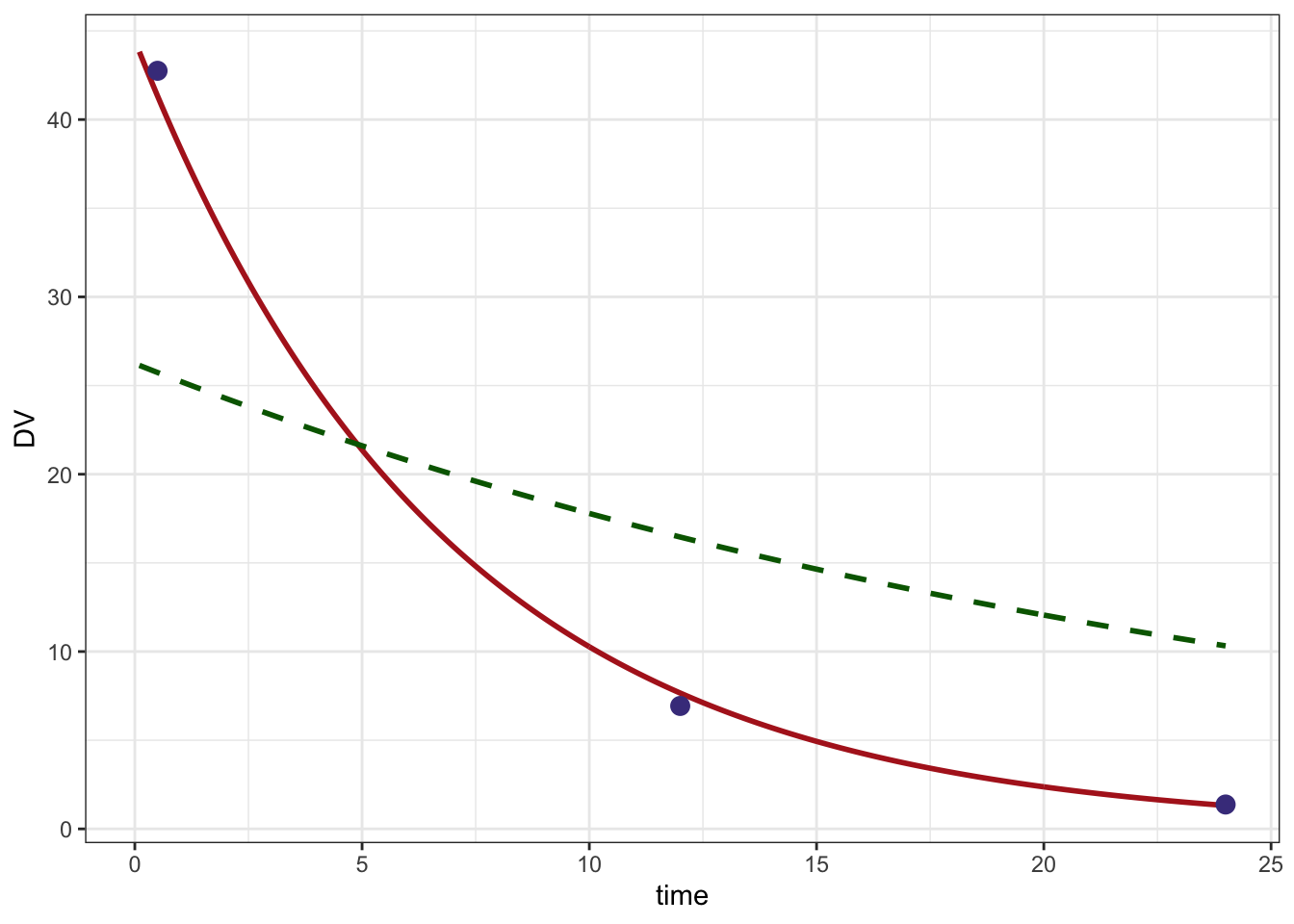

mrgsolve: mrgsolve.github.io | metrum research group: metrumrg.com

Generate MAP Bayes Parameter Estimates